Alexander Sayapin Teacher's site

Дискретная математика для БМЕ18-01 / весна 2020

Posted on Tue 14 April 2020

In Архив.

tags: дискретная математика бме

Коронавирус

В связи с карантином, порядок работы меняется.

В течение карантина вам необходимо будет решить задания, размещенные на этой странице ниже.

При выполнении заданий можно использовать следующие источники:

• Дискретная математика

• Дискретная математика: учебное пособие/ А. В. Саяпин, Т. А. Сливина. - Красноярск: СибГАУ, 2010

• Дискретная математика. Курс лекций

• Ф. А. Новиков Дискретная математика. 2-е изд. – С-Пб.: Питер, 2013 г.

• Эвнин А. Ю. Дискретная математика. Конспект лекций. – Челябинск: ЮУрГУ, 1998.

• В.С. Фомичев Формальные языки, грамматики и автоматы[электр].

• Мозговой М.В. Программирование. Классика программирования: алгоритмы, языки, автоматы.- М.: Наука и техника, 2006.

Решение заданий вам необходимо прислать в виде ссылки на Google Docs.

Для этого вам необходимо:

1. Иметь учетную запись Google (например, почту на gmail).
2. Войти в учетную запись Google
3. Перейти по ссылке на задание, расположенной ниже
4. Нажать кнопку Создать копию
5. Выполнить задание непосредственно в браузере, записывая ответы в предназначенные для них ячейки
6. Нажать кнопку Настройки доступа и выбрать пункт Комментирование
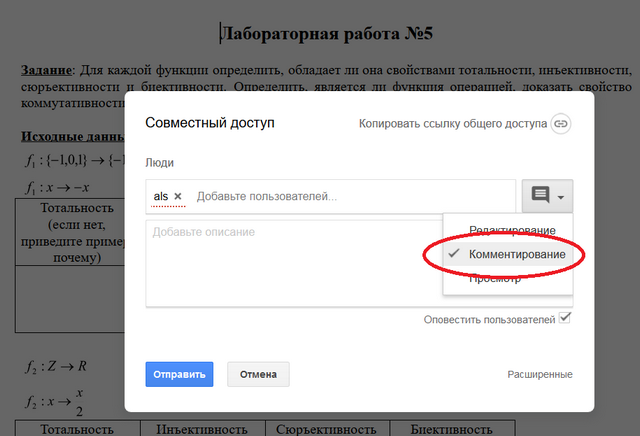
7. В поле Введите имена или адреса эл. почты введите alstutor@gmail.com 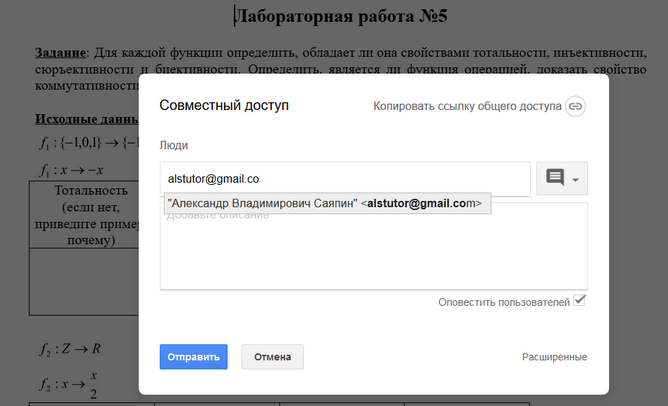и нажмите кнопку Отправить

Если работа принята, в бокноте появится комментарий Принято, в противном случае будет указано, где именно имеются ошибки.

Остальная информация пока остается без изменений.

Список заданий:

• Свойства операций. При выполнении работы можно использовать следующие материалы: Дискретная математика: учебное пособие/ А. В. Саяпин, Т. А. Сливина. - Красноярск: СибГАУ, 2010, стр. 15
• Математическая логика. При выполнении работы можно использовать следующие материалы: Дискретная математика, стр. 40, Дискретная математика: учебное пособие/ А. В. Саяпин, Т. А. Сливина. - Красноярск: СибГАУ, 2010, стр. 21, Дискретная математика. Курс лекций, Ф. А. Новиков Дискретная математика. 2-е изд. – С-Пб.: Питер, 2013 г., стр. 154.
• Графы и их характеристики. При выполнении работы можно использовать следующие материалы: учебник "Дискретная математика", стр. 42, Дискретная математика, пособие "Дискретная математика", стр. 140
• Кратчайший путь в ориентированном ненагруженом орграфе. Прежде, чем решать задание, пришлите мне граф для проверки! При выполнении работы можно использовать следующие материалы: Дискретная математика: учебное пособие/ А. В. Саяпин, Т. А. Сливина. - Красноярск: СибГАУ, 2010, стр. 47-49, 51, Графы для самых маленьких: BFS, Алгоритм Ли, Теория графов: Волновой алгоритм поиска кратчайшего пути. Центр онлайн-обучения «Фоксфорд»
• Кратчайший путь в нагруженом орграфе. При выполнении работы можно использовать следующие материалы: Программирование графов на Python с помощью NetworkX, Дискретная математика: учебное пособие/ А. В. Саяпин, Т. А. Сливина. - Красноярск: СибГАУ, 2010, стр. 53, Ф. А. Новиков Дискретная математика. 2-е изд. – С-Пб.: Питер, 2013 г, стр. 301

Курс дискретной математики рассчитан на 1 семестр, в конце курса предусмотрен дифференцированный зачет.

Итоговая оценка выставляется в соответствии с требованиями балльно-рейтинговой системы (см. критерии оценки на экзамене и систему оценок). Для допуска к экзамену необходимо выполнить и защитить все практические работы (ориентировочно 12 штук) и получить не менее 51 балла в течение семестра.

При изучении курса можно использовать следующую литературу:

• Ф. А. Новиков Дискретная математика для программистов. – С-Пб.: Питер, 2008 г.

• Эвнин А. Ю. Дискретная математика. Конспект лекций. – Челябинск: ЮУрГУ, 1998.

• Мозговой М.В. Программирование. Классика программирования: алгоритмы, языки, автоматы.- М.: Наука и техника, 2006.

Примерные вопросы для изучения:

Примерный список вопросов к экзамену (состав и количество вопросов могут быть откорректированы):

1. Множества. Основные понятия. Действия над множествами.

2. Основные тождества алгебры множеств. Прямое произведение множеств. Свойства прямого произведения.

3. Отношения на множествах, их свойства. Композиция отношений.

4. Функции и отображения. Ядро функции.

5. Алгебраическая операция. Свойства. Единичный и обратный элемент. Единственность существования единичного и обратного элемента.

6. Основные понятия теории графов. Свойства графов.

7. Способы задания графов. Матрицы смежности и инцидентности, их свойства.

8. Компонента связности. Матрицы достижимости, связности, сильной связности.

9. Маршрут. Алгоритм Тери.

10. Поиск минимальных путей в орграфе. Алгоритм “Фронт волны”.

11. Нагруженный граф. Минимальный путь в нагруженном графе, свойства. Поиск минимальных путей в нагруженном орграфе. Алгоритм “Форда - Беллмана”.

12. Эйлеровы циклы (цепи). Алгоритм построения Эйлерова цикла. Гамильтоновы цепи (циклы).

13. Деревья, их свойства. Остовное дерево. Алгоритм выделения остовного дерева связного графа.

14. Цикломатическое число, смысл, свойства. Вектор-цикл. Независимые циклы. Цикловой базис. Наибольшее число независимых циклов в графе. Алгоритм нахождения циклового базиса связного графа.

15. Транспортная сеть. Прикладные задачи, решаемые с помощью теории транспортных сетей.

16. Поток в транспортной сети. Понятие полного потока. Алгоритм построения полного потока.

17. Максимальный поток. Алгоритм построения максимального потока в транспортной сети.