Alexander Sayapin Teacher's site

Дискретная математика для группы БИСВ18-01

Posted on Mon 06 April 2020

In Архив.

tags: дискретная математика бисв

Коронавирус

В связи с карантином, порядок работы меняется.

В течение карантина вам необходимо будет решить задания, размещенные на этой странице ниже.

При выполнении заданий можно использовать следующие источники:

• Дискретная математика

• Дискретная математика. Курс лекций

• Ф. А. Новиков Дискретная математика. 2-е изд. – С-Пб.: Питер, 2013 г.

• Дискретная математика [Электронный ресурс]: учебное пособие/ А. В. Саяпин, Т. А. Сливина, К. В. Сафонов. - Электрон. текстовые дан.. - Красноярск: СибГАУ, 2014.

• NetworkX Notebooks

• В.С. Фомичев Формальные языки, грамматики и автоматы[электр].

• Мозговой М.В. Программирование. Классика программирования: алгоритмы, языки, автоматы.- М.: Наука и техника, 2006.

Решение заданий вам необходимо прислать в виде ссылки на Google Docs.

Для этого вам необходимо:

1. Иметь учетную запись Google (например, почту на gmail).
2. Войти в учетную запись Google
3. Перейти по ссылке на задание, расположенной ниже
4. Нажать кнопку Создать копию
5. Выполнить задание непосредственно в браузере, записывая ответы в предназначенные для них ячейки
6. Нажать кнопку Настройки доступа и выбрать пункт Комментирование
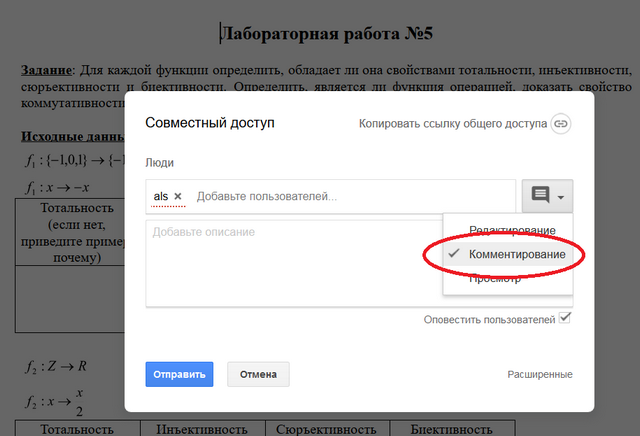
7. В поле Введите имена или адреса эл. почты введите alstutor@gmail.com 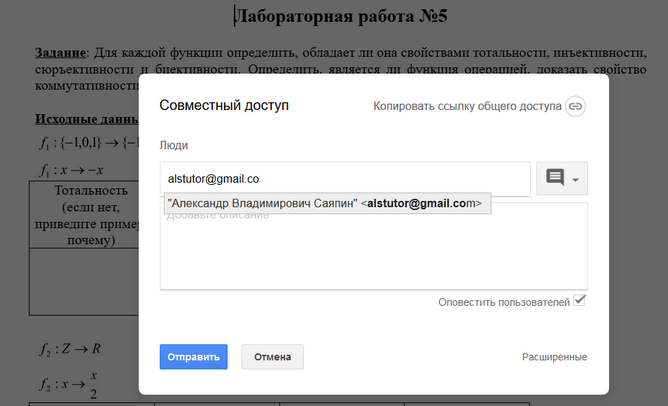и нажмите кнопку Отправить

Если работа принята, в бокноте появится комментарий Принято, в противном случае будет указано, где именно имеются ошибки.

Остальная информация пока остается без изменений.

Список заданий:

• Свойства функций. При выполнении работы можно использовать следующие материалы: Дискретная математика, стр. 26, Дискретная математика: учебное пособие/ А. В. Саяпин, Т. А. Сливина. - Красноярск: СибГАУ, 2010, стр. 15, Ф. А. Новиков Дискретная математика. 2-е изд. – С-Пб.: Питер, 2013 г, стр. 60
• Свойства операций. При выполнении работы можно использовать следующие материалы: Дискретная математика, стр. 40, Дискретная математика: учебное пособие/ А. В. Саяпин, Т. А. Сливина. - Красноярск: СибГАУ, 2010, стр. 21, Дискретная математика. Курс лекций, Ф. А. Новиков Дискретная математика. 2-е изд. – С-Пб.: Питер, 2013 г., стр. 154.
• Математическая логика. При выполнении работы можно использовать следующие материалы: Дискретная математика, стр. 40, Дискретная математика: учебное пособие/ А. В. Саяпин, Т. А. Сливина. - Красноярск: СибГАУ, 2010, стр. 21, Дискретная математика. Курс лекций, Ф. А. Новиков Дискретная математика. 2-е изд. – С-Пб.: Питер, 2013 г., стр. 154.
• Графы и их характеристики. При выполнении работы можно использовать следующие материалы: учебник "Дискретная математика", стр. 42, Дискретная математика, пособие "Дискретная математика", стр. 140

По всем вопросам можно писать на электронную почту (ссылка mail me справа).

Курс дискретной математики рассчитан на 1 семестр, в конце курса предусмотрен экзамен.

Итоговая оценка выставляется в соответствии с требованиями балльно-рейтинговой системы (см. критерии оценки на экзамене).

Для допуска к экзамену необходимо выполнить все работы.

При изучении курса можно использовать следующую литературу:

• Дискретная математика / А. В. Саяпин, Т. А. Сливина ; М-во образования и науки Российской Федерации, Сибирский гос. аэрокосмический ун-т им. М. Ф. Решетнева. - Красноярск : Сибирский гос. аэрокосмический ун-т имени акад. М. Ф. Решетнева, 2010.

• Ф. А. Новиков Дискретная математика для программистов. – С-Пб.: Питер, 2008 г.

• Эвнин А. Ю. Дискретная математика. Конспект лекций. – Челябинск: ЮУрГУ, 1998.

Примерный список вопросов к экзамену (состав и количество вопросов могут быть откорректированы):

1. Множества. Основные понятия. Действия над множествами.

2. Основные тождества алгебры множеств. Прямое произведение множеств. Свойства прямого произведения.

3. Отношения на множествах, их свойства. Обратное отношение.

4. Функции и отображения. Свойства функций.

5. Алгебраическая операция. Свойства. Единичный и обратный элемент и их поиск.

6. Основные понятия математической логики. Законы логики. Понятие высказывания. Логические операции над высказываниями.

7. Математическая логика Дизъюнктивная/конъюнктивная нормальная форма. Свойства совершенства. Получение СДНФ.

8. Основные понятия теории графов. Свойства графов.

9. Способы задания графов. Матрицы смежности и инцидентности, их свойства.

10. Маршрут в графе. Его свойства. Маршруты, цепи и простые цепи.

11. Понятие минимального пути в графе. Поиск минимальных путей в орграфе. Алгоритм “Фронт волны” .