Alexander Sayapin Teacher's site
Дискретная математика для ТБ18-01 / весна 2020
Posted on Tue 14 April 2020
In Архив.
tags: дискретная математика тб
Коронавирус
В связи с карантином, порядок работы меняется.
В течение карантина вам необходимо будет решить задания, размещенные на этой странице ниже.
При выполнении заданий можно использовать следующие источники:
-
Дискретная математика: учебное пособие/ А. В. Саяпин, Т. А. Сливина. - Красноярск: СибГАУ, 2010
-
Ф. А. Новиков Дискретная математика. 2-е изд. – С-Пб.: Питер, 2013 г.
-
Дискретная математика [Электронный ресурс]: учебное пособие/ А. В. Саяпин, Т. А. Сливина, К. В. Сафонов. - Электрон. текстовые дан.. - Красноярск: СибГАУ, 2014.
-
Эвнин А. Ю. Дискретная математика. Конспект лекций. – Челябинск: ЮУрГУ, 1998.
-
В.С. Фомичев Формальные языки, грамматики и автоматы[электр].
-
Мозговой М.В. Программирование. Классика программирования: алгоритмы, языки, автоматы.- М.: Наука и техника, 2006.
Решение заданий вам необходимо прислать в виде ссылки на Google Docs.
Для этого вам необходимо:
- Иметь учетную запись Google (например, почту на gmail).
- Войти в учетную запись Google
- Перейти по ссылке на задание, расположенной ниже
- Нажать кнопку Создать копию
- Выполнить задание непосредственно в браузере, записывая ответы в предназначенные для них ячейки
- Нажать кнопку Настройки доступа и выбрать пункт Комментирование
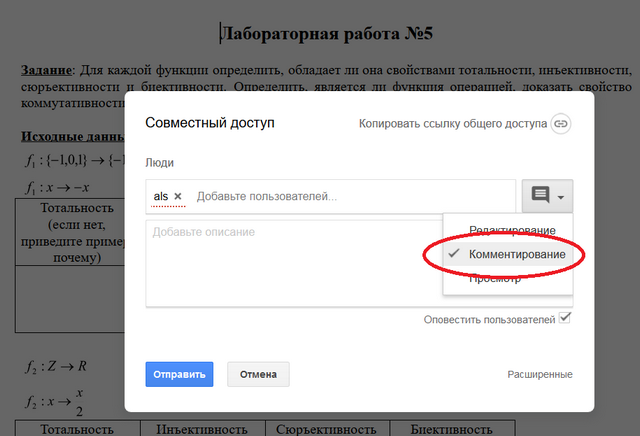
- В поле Введите имена или адреса эл. почты введите alstutor@gmail.com
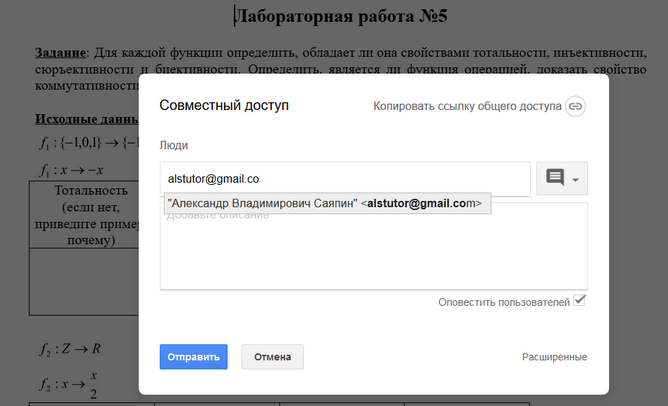и нажмите кнопку Отправить
Если работа принята, в бокноте появится комментарий Принято, в противном случае будет указано, где именно имеются ошибки.
Остальная информация пока остается без изменений.
Список заданий:
- Кратчайший путь в нагруженом орграфе. При выполнении работы можно использовать следующие материалы: Программирование графов на Python с помощью NetworkX, Дискретная математика: учебное пособие/ А. В. Саяпин, Т. А. Сливина. - Красноярск: СибГАУ, 2010, стр. 53, Ф. А. Новиков Дискретная математика. 2-е изд. – С-Пб.: Питер, 2013 г, стр. 301
- Транспортная сеть. При выполнении работы можно использовать следующие материалы: Дискретная математика: учебное пособие/ А. В. Саяпин, Т. А. Сливина. - Красноярск: СибГАУ, 2010, стр. 66, Ф. А. Новиков Дискретная математика. 2-е изд. – С-Пб.: Питер, 2013 г, стр. 292
- Формальные грамматики. При выполнении работы можно
использовать следующие материалы: текст по формальным грамматикам, Дискретная математика: учебное пособие/ А. В. Саяпин, Т. А. Сливина. - Красноярск: СибГАУ, 2010, стр. 77, В.С. Фомичев Формальные языки, грамматики и автоматы[электр].
Для выполнения работы так же необходима программа JFLAP, так же доступная с этого сайта, для запуска необходима установленная на компьютере JAVA.
Описание работы с программой имеется в методичке.
- Список адресов для самопроверки, допустимые:
- a@a.a
- aa@a.a
- a@aaaa.a
- a@a.aaaa
- a.a@a.a
- a.a@a.a.a
- a.a.a@a.a
- a@a.aa.a
- a@aa.aa.aa
- Список адресов для самопроверки, недопустимые:
- a
- aa
- a@
- @a
- a@a
- a@a.
- a@.a
- a@a.
- a.@a.a
- .a@a.a
- a..a@a.a
- a.a@a..a
- a.a@a.a.a.
- Список так же доступен в виде файла, можно использовать для проверки в JFLAP, выбрав в меню пункты Input/Multiple Brute Force Parse, и нажав кнопку Load Inputs. Учтите, проверка потребует времени, поскольку производится методом брутфорса (фактически, полного перебора всех правил с проверкой их применимости на каждом этапе разбора)
- Список адресов для самопроверки, допустимые:
- Классификация грамматик и их представления. При выполнении работы можно использовать следующие материалы: Дискретная математика: учебное пособие/ А. В. Саяпин, Т. А. Сливина. - Красноярск: СибГАУ, 2010, стр. 86-88, В.С. Фомичев Формальные языки, грамматики и автоматы (1.3. Типы формальных грамматик, 1.4.1. Форма Бекуса-Наура, 1.4.3. Синтаксическая диаграмма)
- Конечные автоматы-распознаватели. При выполнении работы можно использовать следующие материалы: Дискретная математика: учебное пособие/ А. В. Саяпин, Т. А. Сливина. - Красноярск: СибГАУ, 2010, стр. 102-105., Дискретная математика: учебное пособие/ В.М. Пестриков, В.С.Дудкин, Г.А.Петров. - Санкт-Петербург: 2013, стр. 1-6.
По всем вопросам можно писать на электронную почту (ссылка mail me справа).
Курс дискретной математики рассчитан на 2 семестра, в конце курса предусмотрен экзамен.
Итоговая оценка выставляется в соответствии с требованиями балльно-рейтинговой системы (см. критерии оценки на экзамене). Для допуска к экзамену необходимо выполнить и защитить все практические работы и получить не менее 51 балла в течение семестра.
При изучении курса можно использовать следующую литературу:
-
Ф. А. Новиков Дискретная математика для программистов. – С-Пб.: Питер, 2008 г. (1 семестр, 2 семестр)
-
Эвнин А. Ю. Дискретная математика. Конспект лекций. – Челябинск: ЮУрГУ, 1998. (1 семестр)
-
В.С. Фомичев Формальные языки, грамматики и автоматы[электр]. (2 семестр)
-
Мозговой М.В. Программирование. Классика программирования: алгоритмы, языки, автоматы.- М.: Наука и техника, 2006. (2 семестр)
Примерный список вопросов к экзамену (состав и количество вопросов могут быть откорректированы):
-
Множества. Основные понятия. Действия над множествами.
-
Основные тождества алгебры множеств. Прямое произведение множеств. Свойства прямого произведения.
-
Покрытие и разбиение. Отношение эквивалентности и отношение частичного порядка.
-
Отношения на множествах, их свойства. Композиция отношений. Обратное отношение.
-
Функции и отображения. Ядро функции. Свойства функций.
-
Алгебраическая операция. Свойства. Единичный и обратный элемент и их поиск.
-
Основные понятия математической логики. Законы логики. Понятие высказывания. Логические операции над высказываниями.
-
Формула алгебры логики. Равносильные формулы алгебры логики. Тождественно-истинные и тождественно-ложные формулы.
-
Алгебра Буля. Функции Буля. Представление функции алгебры логики в виде формулы алгебры логики.
-
Функции алгебры логики, их связь с дизъюнктивной/конъюнктивной нормальной формой. Свойства совершенства. Получение СДНФ.
-
Рассуждения. Логический вывод. Подтверждение правильности логического вывода.
-
Математическая логика. Логический вывод. Основная теорема логического вывода.
-
Логика предикатов. Понятие предиката. Связь предикатов и высказываний.
-
Логика предикатов. Классификация предикатов. Свойства предикатов.
-
Логика предикатов. Предваренная нормальная форма, ее использование и получение.
-
Логика предикатов. Скулемовская нормальная форма, ее использование и получение.
-
Логика предикатов. Алгоритм унификации. Вывод в логике предикатов.
-
Основные понятия теории графов. Свойства графов.
-
Способы задания графов. Матрицы смежности и инцидентности, их свойства.
-
Маршрут в графе. Его свойства. Маршруты, цепи и простые цепи.
-
Понятие минимального пути в графе. Поиск минимальных путей в орграфе. Алгоритм “Фронт волны”.
-
Нагруженный граф. Минимальный путь в нагруженном графе, свойства. Поиск минимальных путей в нагруженном орграфе. Алгоритм “Форда - Беллмана”.
-
Деревья, их свойства. Остовное дерево. Алгоритм выделения остовного дерева связного графа.
-
Транспортная сеть. Прикладные задачи, решаемые с помощью теории транспортных сетей. Основные понятия теории транспортных сетей.
-
Транспортная сеть. Поток в транспортной сети. Понятие полного потока. Алгоритм построения полного потока.
-
Максимальный поток в транспортной сети. Алгоритм построения максимального потока в транспортной сети.
-
Формальные языки, грамматики и автоматы. Язык, строка, алфавит. Основные понятия.
-
Формальные языки. Понятие формальной грамматики. Классификация грамматик. Примеры грамматик.
-
Автоматные грамматики и конечные автоматы. Распознаватель. Устройство, назначение, порядок работы.
-
Теория автоматов. Конечные автоматы. Детерминированные и недетерминированные конечные автоматы. Алгоритм преобразования недетерминированного автомата в детерминированный.
-
Контекстно-свободные грамматики, их особенности. Распознаватель с магазинной памятью, порядок работы.